Triangles ⇒⇒ Exercise 7.3

Question 1

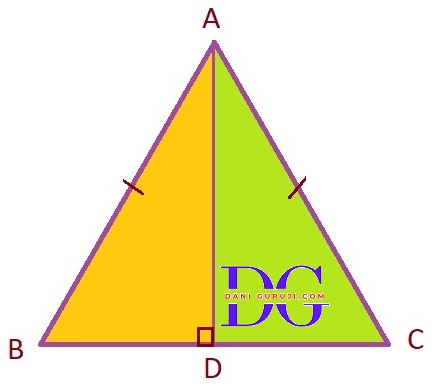
ΔABC and ΔDBC are two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig.). If AD is extended to intersect BC at P, show that
(i) Δ ABD $\cong$ Δ ACD
(ii) Δ ABP $\cong$ Δ ACP
(iii) AP bisects $\angle $A as well as $\angle $D.
(iv) AP is the perpendicular bisector of BC.

Solution :

Part (i): Δ ABD $\cong$ Δ ACD

We are given that Δ ABC and Δ DBC are isosceles triangles on the same base BC, with vertices A and D on the same side of BC.

Therefore, in Δ ABC, AB = AC

And in Δ DBC, DB = DC

Consider the Δ ABD and Δ ACD:

⇒ AB = AC

( Given, Equal sides of isosceles Δ ABC )

⇒ DB = DC

( Given, Equal sides of isosceles Δ DBC )

AD = AD

( This is a common side for both triangles.)

∴ Δ ABD $\cong$ Δ ACD

( by the SSS congruence rule. )

Part (ii): Δ ABP $\cong$ Δ ACP

In part (i), we know that Δ ABD $\cong$ Δ ACD

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, $\angle $BAD = $\angle $CAD.

Consider the Δ ABP and Δ ACP:

⇒ AB = AC

( Given, Equal sides of isosceles Δ ABC )

⇒ $\angle $BAP = $\angle $CAP

( Since $\angle $BAD = $\angle $CAD, and P is on the extension of AD, we can write $\angle $BAP = $\angle $CAP )

AP = AP

( This is a common side for both triangles.)

∴ Δ ABP $\cong$ Δ ACP

( by the SAS congruence rule. )

Part (iii): AP bisects $\angle $A as well as $\angle $D

In part (i), we know that Δ ABD $\cong$ Δ ACD

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, $\angle $BAD = $\angle $CAD.

Since P lies on the extension of AD, this means that line segment AP bisects $\angle $A

From the congruence in part (i), we also know that corresponding angles are equal.

Therefore, $\angle $ADB = $\angle $ADC.

This means that line segment AD bisects $\angle $D.

Since P lies on the extension of AD, we can say that

AP bisects $\angle $A as well as $\angle $D.

Part (iv) AP is the perpendicular bisector of BC

In part (ii), we know that Δ ABP $\cong$ Δ ACP

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, BP = CP
and $\angle $APB = $\angle $APC.

Since $\angle $APB and $\angle $APC are a linear pair, their sum is 180°

$\angle $APB + $\angle $APC = 180°

2 $\angle $APB = $ { 180° }$

$\angle $APB = $ { 180° \over 2}$

$\angle $APB = $ { 90° }$ = $\angle $APC

This means that AP is perpendicular to BC

Also, we established that BP = CP. This means that P is the midpoint of BC, so AP bisects BC

Since AP is both perpendicular to BC and bisects BC, we can conclude that AP is the perpendicular bisector of BC.

Question 2

AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
(i) AD bisects BC
(ii) AD bisects $\angle $A

Solution :

(i) AD bisects BC

We are given that Δ ABC is an isosceles triangle with AB = AC, and AD is an altitude to BC.

This means that AD is perpendicular to BC,

So,$\angle $ ADB = $\angle $ ADC = 90°

Consider the Δ ABD and Δ ACD:

⇒ AB = AC

( Given, Equal hypotenuse of a right-angled triangle )

⇒ $\angle $ ADB = $\angle $ ADC = 90°

( Given, since AD is an altitude )

AD = AD

( This is a common side for both triangles.)

∴ Δ ABD $\cong$ Δ ACD

( by the RHS congruence rule. )

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, BD = CD.
This shows that D is the midpoint of BC, and thus, AD bisects BC.

Part (ii) AD bisects $\angle $A

In part (i), we know that Δ ABD $\cong$ Δ ACD

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, $\angle $BAD = $\angle $CAD.

This equality of angles means that AD divides $\angle $A into two equal parts, thus AD bisects $\angle A $ .

Question 3

Two sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of Δ PQR. Show that :
(i) Δ ABM $\cong$ Δ PQN
(ii)Δ ABC $\cong$ Δ PQR

Solution :

We are given that Δ ABC and △ PQR, where AB = PQ, BC = QR and median AM = PN .

AM is the median of △ ABC

∴ BM = CM = ${1 \over 2}$ BC

Also, PN is the median of △ PQR

∴ QN = RN = ${1 \over 2}$ QR

Since we are given that BC = QR,

we can conclude that ${1 \over 2}$BC = ${1 \over 2}$QR , which means BM = QN.

(i) Δ ABM $\cong$ Δ PQN

Consider the Δ ABM and Δ PQN:

⇒ AB = PQ

( Given,)

⇒ AM = PN

( Given, )

⇒ BM = QN

( This is proved above.)

∴ Δ ABM $\cong$ Δ PQN

( by the SSS congruence rule. )

Since we have proved that Δ ABM $\cong$ Δ PQN

This means that corresponding parts of congruent triangles are equal (CPCT).

Therefore, $\angle $B = $\angle $Q.

(ii) Δ ABC $\cong$ Δ PQR

Consider the Δ ABC and Δ PQR:

⇒ AB = PQ

( Given,)

⇒ BC = QR

( Given, )

⇒ $\angle $B = $\angle $Q

( This is proved above.)

∴ Δ ABC $\cong$ Δ PQR

( by the SAS congruence rule. )

Question 4

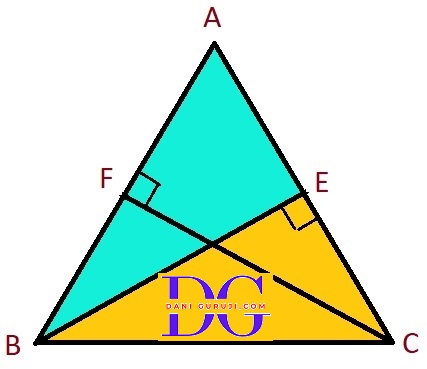
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.

Solution :

From given figure, It is given that

Altitudes, BE = CF,

CF is an altitude to side AB, which means = $\angle $AFC = $\angle $BFC = 90°

BE is an altitude to side AC, which means = $\angle $ AEB = $\angle $ BEC = 90°

Consider the two right-angled triangles ΔBEC and Δ CFB

⇒ BE = CF

( Given that the altitudes are equal. )

⇒ $\angle $ BEC = $\angle $ BFC

( Both are 90°. )

⇒ BC = BC

( Since this hypotenuse side is common to both triangles, )

∴ ΔBEC $\cong$ Δ CFB

( by the RHS congruence rule. )

Since the two triangles are congruent, their corresponding parts are also equal (CPCT). Therefore, the angles opposite the equal sides must be equal.

Since BE = CF and the triangles are congruent, the angles opposite to these sides must be equal.

So, $\angle $FCB = $\angle $EBC, which means $\angle $C = $\angle $B.

Since the base angles of △ABC are equal ( $\angle $C = $\angle $B), the sides opposite to these angles must also be equal. This means AB = AC.

A triangle with two equal sides is an isosceles triangle. Therefore, △ABC is an isosceles triangle.

Question 5

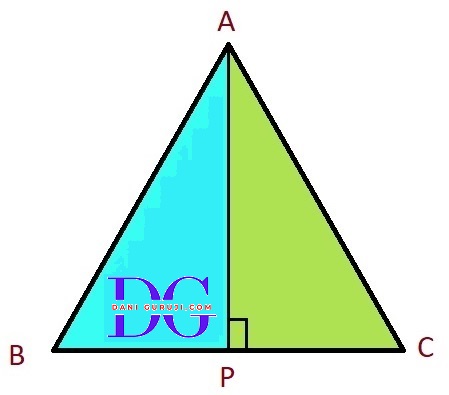
ABC is an isosceles triangle with AB = AC. Draw AP ⊥ BC to show that $\angle $B = $\angle $C.

Solution :

From given figure, It is given that

AP is the perpendicular of BC. This means that

$\angle $APB = $\angle $APC = 90°

And AB = AC.

Consider the triangles Δ APB and Δ APC

⇒ AB = AC

( Given,Equal hypotenuse of a right-angled triangle. )

⇒ $\angle $APB = $\angle $APC

( Both are 90°. )

⇒ AP = AP

( Common side to both triangles. )

∴ Δ APB $\cong$ Δ APC

( by the RHS congruence rule. )

Since the two triangles are congruent, their corresponding parts must be equal

$\angle $B = $\angle $C. (By C.P.C.T.)

By definition, a triangle with two equal sides is an isosceles triangle. Since we have shown that

Therefore, $\angle $B = $\angle $C. This proves that the base angles of an isosceles triangle are equal..